Acid strength

Equilibrium: Acid strength

The ionic power of a strong electrolyte consists solely of singly charged ions is identical with its completely total molar salt concentration. More the ionic strength of a solution, the maximum is the charge in the ionic atmospheres. Strong and weak in this context are used to understand the capability of a substance to ionize in a solution, mainly water.

Water is capable of autoionizing. Because both the “acid” and “base” are water, the degree of dissociation orauto-ionization is very slight.

For water, the concentration of the dissociated products are constant, Kw.

While Kw is constant, the concentration of hydronium ion can change greatly.
It is this [H3O⁺¹] that chemists measure as pH

pH = -log[H3O⁺¹]

Every acid has a conjugate base pair that is formed with reacted with water. Likewise, every base has a conjugate base pair. This means that we can deduce the relative strength of an acid or a base by K_a or K_b value. Recall that K_w=K_a x K_b where Kw = 1.00 x 10^-14

An acid’s strength is measured as its dissociation constant, Ka.
So, imagine an acid, Ka:

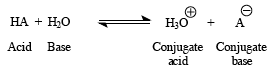
Most organic acids are quite weak and have Ka values between 10^-2 and 10^-60.To make it easier to compare this very wide range of values, Ka is often converted to pKa, a logarithmic scale:

Since this scale is inverse logarithmic but lower the pKa the stronger the acid.

The larger the Ka value stronger the acid’s strength. Strong acids have pKa values between at zero or below.

By using pK_a values, we can express the strength of an acid (i.e. its ease of dissociation) with reference to the pH scale. If K_a value is large, then pK_ais a low numerical value. E.g.,

• Hydrochloric acid, HCl has a pK_a = -3
• Acetic acid, CH₃COOH has a pK_a = 4.77

Figure 1: Relationship between acid strength and bond strength

A strong acid is largely, or completely, dissociated, and which therefore has a high K_a value (and low pKa). A weak acid is only slightly dissociated in solution and has a low K_a value.

So bases are stronger when their conjugate acids have lower Ka values; or higher pKa values.

An interesting and extremely useful relationship between pH and pK_a can be obtained simply by taking logarithms (to the base 10) of the previous equation:

log₁₀K_a = log₁₀[H⁺] + log₁₀[A^– ] – log₁₀[HA]

Therefore

-log₁₀[H⁺] = -log₁₀K_a + log₁₀[A^–] – log₁₀[HA]

Note: log a – log b = log (a/b)

giving the Henderson-Hasselbalch equation:

Hence, if we consider the situation where the acid is one-half (50%) dissociated, or where

[A^–] = [HA]

(that is 50% negatively charged and 50% uncharged)

then, substituting in the Henderson-Hasselbalch Equation

pH = pKa + log(A^–/HA)

pH = pKa + log(1)

pH = pKa + 0

pH = pKa

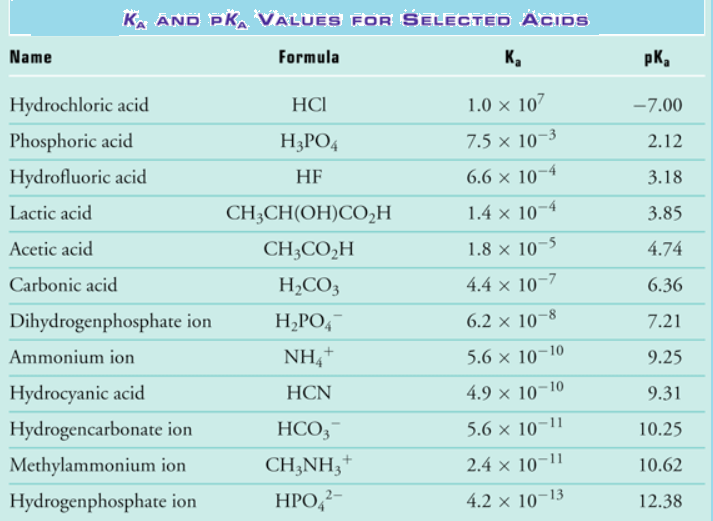
Fig : Strength of acid and bases in terms of Ka and pKa values