Molecular orbital theory of homonuclear diatomic molecules (qualitative idea only)
Molecular Orbitals for Homonuclear Diatomics
As long as the specific molecular orbitals forms (their dependency on R and Z in the cylindrical coordination system) vary for each and every molecule, their dependency on an angle ‘f’ due to the represented by quantum number L and their behavior of G or U w.r.t to inversion are entirely determined by system’s geometry. These properties are generally known to the whole of molecular orbitals specified for “homonuclear diatomic molecules”.
The homonuclear diatomic molecules involve elements like hydrogen (H2), nitrogen (N2), oxygen (O2), and all halogens.
Further, the comparative orbital energies’ order is identical for almost all the homonuclear diatomic molecules. In this way, there’s a probability we can construct the molecular orbital energy level diagram, exactly similar to those used in the periodic table to create electronic configurations of atoms.
The molecular orbital energy level diagram (Figure 1) is as basic for understanding the electronic structure of diatomic molecules as the equivalent atomic orbital diagram is for understanding the atoms.
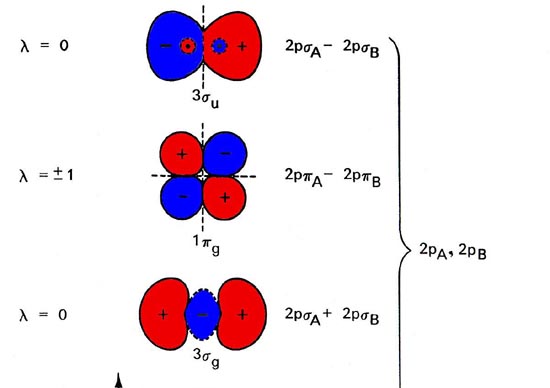
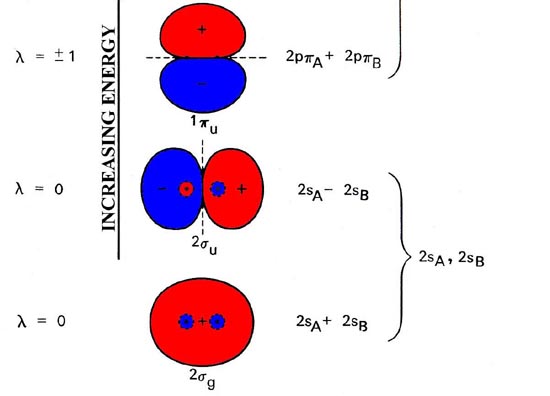
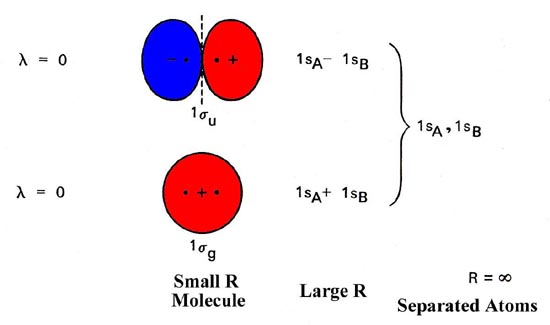
Fig 1
Fig. 1. Energy level diagram of molecular orbital for homonuclear diatomic molecules indicates the interrelationship of molecular orbitals along with atomic orbitals of separated atoms. The simplified representation of molecular orbitals is to describe their common forms and the nodal properties (nodes are represented by the dashed lines). Only a single component of degenerated 1pu and 1pg orbital is given.
The 2nd component is exactly alike in every case but there has been a rotation of 90 ° out of the plane. The order of orbital energy levels depicted in the figure usually goes for all homonuclear diatomic molecules, having an exception in the energy levels for 3sg and 1pu orbitals, whose comparative sequence is reversed for molecules after C2.
Molecular orbitals display the common properties identical to atomic orbits, which includes a nodal structure. Nodal properties of orbitals are depicted in Figure 8-4. Note that the nodal properties rightly represent the G and U character of orbitals.
The reverse of g orbital interchanges areas like sign and what’s unchanged is the orbital. Also, the inversion of ‘u’ orbital switch the positive areas with negative areas and the orbital is converted to sign.
Now, the Molecular Orbital Description for Homonuclear Diatomic molecules
Hydrogen molecule, H2:
The Hydrogen molecule is made up of 1s1 atomic orbits of 2 atoms. They result in two molecular orbitals that are σ(1s) & σ*(1s). These two electrons will have molecular orbital bonding of σ(1s), but having opposite spin. “Antibonding molecular orbital” remain empty in this case. Molecules’ electronic configuration is σ (1s2) 1 * (1s0).
B.O – Bond Order
Bond Order = ½ [Nb – Na] = [2-0]/2 = 1.0
Since its Bond Order is 1.0 therefore it exists and is stable.
Molecular Orbital Diagram of H2 Molecule:
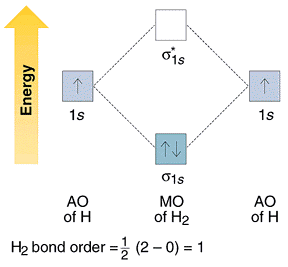
Molecular Orbital Theory for Homonuclear Diatomic
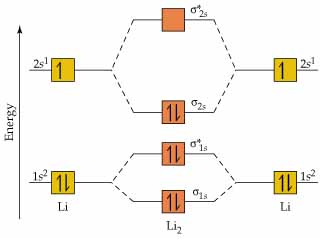
Molecules Lithium molecule (Li2):
The formation of Lithium (Li) molecule is made possible by the overlapping of two lithium atoms and each consisting of electronic configuration 1s2 2s1.
So, we are having a total of 6 electrons which needs to be accommodated in four molecular orbitals, namely, σ1s, σ*1s, σ2s, and σ*2s. Thus, the electronic configuration of molecular orbital of Li2 molecule is σ1s2 σ*1s2 σ2s2 = KK σ2s2.
Since the innermost shell of filled molecular orbitals- σ1s and σ *1s don’t make their contribution to the bonding and is occasionally depicted as KK which shows that K-shell is filled completely.
Bond order = 1/2 (Nb – Na) = 1/2 (4 – 2) = 1/2 (2 – 0) = 1
Molecular Orbital Diagram of Li2 Molecule: