Chemical Thermodynamics: Standard enthalpy of ionization
The quantity of energy that is associated with an isolated gaseous atom in its ground electronic state that absorbs energy to produce an electron and for a cation is called ionization energy . To break free from the attractive force of the atomic nucleus, an electron requires which may be supplied from external sources.
For example,
1/2O2(g) O+(g) +e–
This energy is expressed in kJ/mol and it is the energy required to remove one mole of an electron from an element to produce one mole of isolated gaseous atoms.
Likewise,
X(g) → X+(g) + e– ;first ionisation energy
X+(g) → X2+(g) + e– ;second ionisation energy
X2+(g) → X3+(g) + e– ;third ionisation energy
Second and third ionization energies are more endothermic than first because the electrons become closer to the nucleus
Alternatively, electron affinity () or electron gain affinity is the energy change associated with the addition of one mole of electrons to one mole of isolated atoms or ions in their gaseous state.
Likewise,
X(g) + e– → X–(g) ;first electron affinity
X–(g) + e– → X2–(g) ;second electron affinity
When a weak acid or base reacts with a strong acid or base, some heat energy is released due to incomplete ionization of solutes in the solution. Here, some heat is consumed in ionizing the weak acids and base. For example,
HCN + Na+OH– Na+CN– + H2O ; ∆H=-12.13 kJ/mol
CH3COOH + Na+OH– Na+COO– + H2O ; ∆H=-55.23kJ/mol
Likewise, as per Hess’s Law, the enthalpy of the reaction is the sum of ionization energy and neutralization energy.
A Born-Haber cycle is a classic example of enthalpy as a state function:
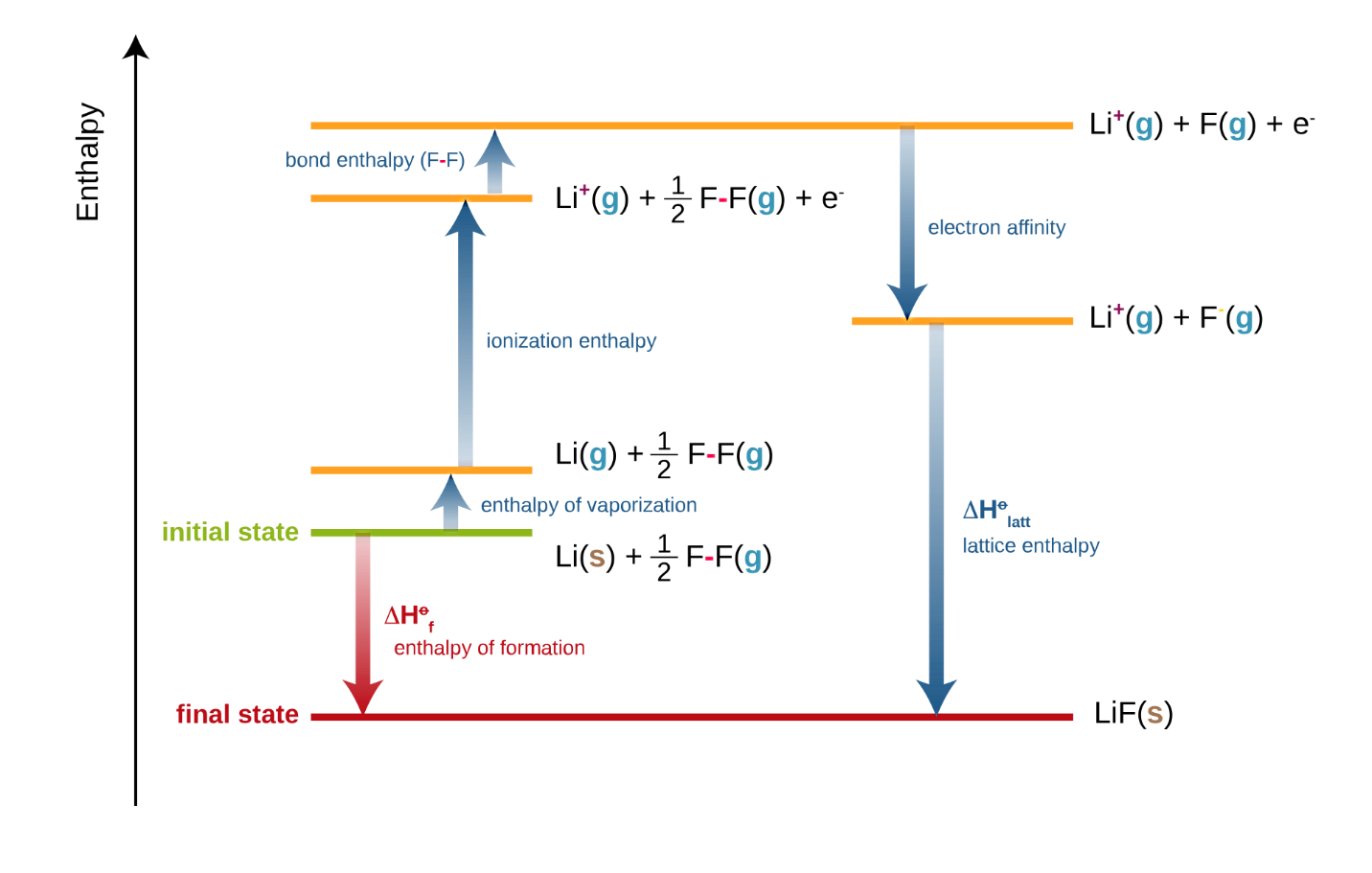
Figure : Born-Haber cycles are enthalpy cycles that show how ionic compounds are formed from their elements. Born-Habe cycle of LiF is shown above
At each stage of the Born-Haber cycle, one enthalpy change occurs. Here, we can apply the Hess’s law of summation to calculate any missing quantity of energy. Various processes involved in Born-Haber Cycle including Electron affinity, Ionization energy, Sublimation energy, Heat of formation, Dissociation energy etc.
Here, Lattice enthalpy is the enthalpy change that accompanies the formation of one mole of an ionic compound from its gaseous ions under standard conditions.
Eg. Li+ (g) + F–(g) LiF (s)
Other enthalpy changes are discussed previously.
To use a Born-Haber cycle, the starting point and the destination are given by the question’s instructions. You need to add all the quantities along the alternative route, considering whether the energy change is negative or positive in the direction you are going. Hence, to calculate an unknown quantity in the Born-Haber cycle, keep in mind that
Heat of formation= Heat of atomization+ (sum of Ionization energies) + (sum of Electron affinities) +Dissociation energy+ Lattice energy
Put a negative sign for any energy that is released and a positive sign of any energy that is absorbed by the system. The enthalpy of formation equals to the sum of all the other steps. So, if we are missing only 1 piece of data we can always work it out using the Born-Haber cycle