The Bohr’s Model failed in explaining concepts regarding the spectrum of different atoms, splitting of spectral lines in electric as well as magnetic field. In order to overcome the imperfection of Bohr’s atomic model, efforts were made to make a general model for atoms.
Louis de Broglie a French physicist, in 1924 gave his theory in which he said just like light electrons have properties of waves and particles. This nature was called as dual behavior. To apply it to all types of matter he rearranged labels of Plank-Einstein relation. After all the observation de Broglie obtained a relation between momentum of matter and wavelength. This relation is known as de Broglie wavelength. It specifically shows the wave nature of electrons.
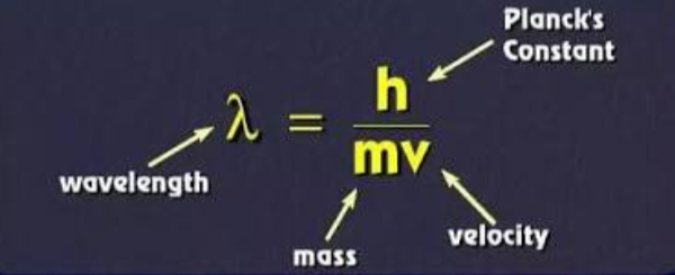
I.e. λ = h/mv (de Broglie equation)
Derivation of de Broglie equation:
Let the energy of a photon to be in terms of its frequency v.
So, E = hv -eq (1)
Where:
E= Energy
m= mass
c= speed of light
The theory of relativity provides a different new aspect in terms of velocity of light. In this new expression, m refers to the relativistic mass of light. Relativistic mass is non-zero because it is travelling with a velocity c. It can be zero only when it is in rest.
E = mc2 -eq (2)
Where:
E= Energy
h= Planck’s constant (6.62607 x 10-34 J s)
v= frequency
Equate the above two equations i.e. (eq 1 and 2) Remember the expression relating to the frequency and wavelength of a photon.
On comparing, de Broglie disagree that a particle having non-zero rest mass m and velocity v would have a wavelength given by:
λ = h/mv
Where h= Planck’s constant
λ= wavelength
m= mass of particle moving at velocity v
Since, mv=p
Where p= particle’s momentum
So now, the de Broglie relation is:
λ = h/p
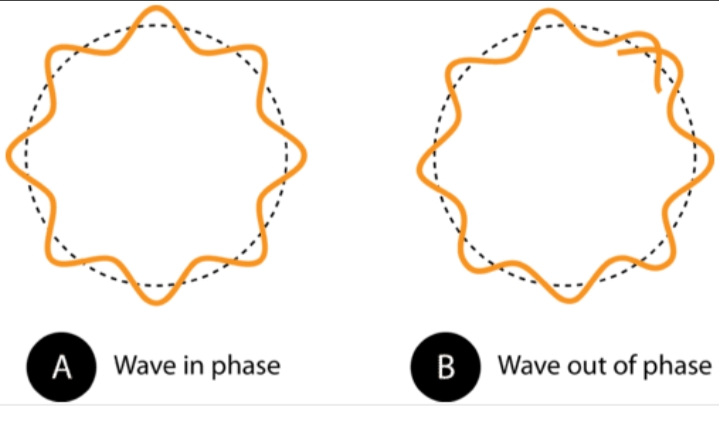
De Broglie relationship is explained by diffraction of electrons beam. Since diffraction is property of waves. Electron microscope is an instrument which demonstrate this fact. Therefore, every moving object has a wavelike character.
De Broglie Wavelength Formula:
As you know in some conditions, light behaves as a wave, whereas in others, it behaves like particles. The particles of light are called photons, and they can be understood as waves and particles too. Louis de Broglie (1892-1987) developed this formula to relate this dual wave and particle behavior. It can also be appended to other particles, like electrons or protons. The formula is the relation of the wavelength to the momentum of a wave or particle.
For particles that have mass i.e.(electrons or protons) but not photons, there is another structure of the de Broglie wavelength formula. The momentum of a particle at non-relative speeds is equal to its rest mass (m) multiplied by its velocity (v).
Units:
De Broglie wavelength’s unit is meters. It is expressed in nanometers (1 nm = 10(-9) m) or angstroms because it is very small.
λ = the de Broglie wavelength (m)
p = momentum of a particle ()
m = mass of a particle (kg)
v = velocity of a particle (m/s)
h = Planck’s constant ()